The Solo mobile app allows our users to track their miles automatically as they drive. Using business data obtained from the platforms our users work on, along with location data from their mobile devices, we are able to infer which portions of their drives are work-related vs personal. This allows our users a host of benefits including mileage tracking that our users can use to save major money when filing their taxes.

Computing miles can be a challenging technical task for many reasons! We need to consider our user’s battery life and data usage while maintaining accuracy. A case in point is the notorious example from DoorDash which provided users a distance as the crow flies between start and end points. Needless to say, this ended with Dashers leaving significant money on the table.

A recent fix we made to our algorithm to improve accuracy on an edge case highlights some of the challenges of geo programming.

We compute the distance across a complete list of geo points, using the Haversine distance between each and summing these up. While this tends to be a pretty accurate method, it is not without challenges. A couple of inter-related challenges that we’ve been dealing with.

Challenge 1: How to compute distance when a user is not leaving the app on for the entire duration of a ride
The first case can be understood by a simple example. Say Kate drives Lyft and has the Solo app on as she is having breakfast at home in Redmond while getting ready to drive. She then, before heading to a pickup zone near Seattle downtown, closes out of the app to preserve battery. Let’s say she is 16 miles away from Seattle. When she reaches the pickup zone and opens the Lyft app to accept rides, she also turns on Solo before completing several Lyft rides in and around Seattle.

Now on the backend, we see a few geo points for her from her home location in Redmond, and then a large number of geo points in Seattle. And—this is the important point—we see a jump between a point in Redmond and a point in Seattle. It would be incorrect to calculate the distance between these two points unless Kate was flying (and we would be winging it haha—sorry it was too good to resist).

Challenge 2: How to ignore inaccurate geo points sent by the mobile app
At times the phone can get confused and send us a location that is miles out. Exactly why this happens is still somewhat of a mystery, but we do know that when the phone is not moving the accuracy can be low. I have seen locations as far south as near GooglePlex, CA when it should be in/around Seattle.

We fixed the second challenge first (we are big on structure and process here), Jokes aside, we ran into the second challenge before we hit the first. Though the second challenge is more common than the first, the solution to Challenge 2 has an effect on 1.

Working Through the Challenges
We fixed challenge 2 by running a large number of tests where we measured and tracked the steadily accumulating distance across the trip. We then zoomed in on data points where there was a significant jump. To get a sense of the actual geo points on a map where the location was far off we used BatchGeo.

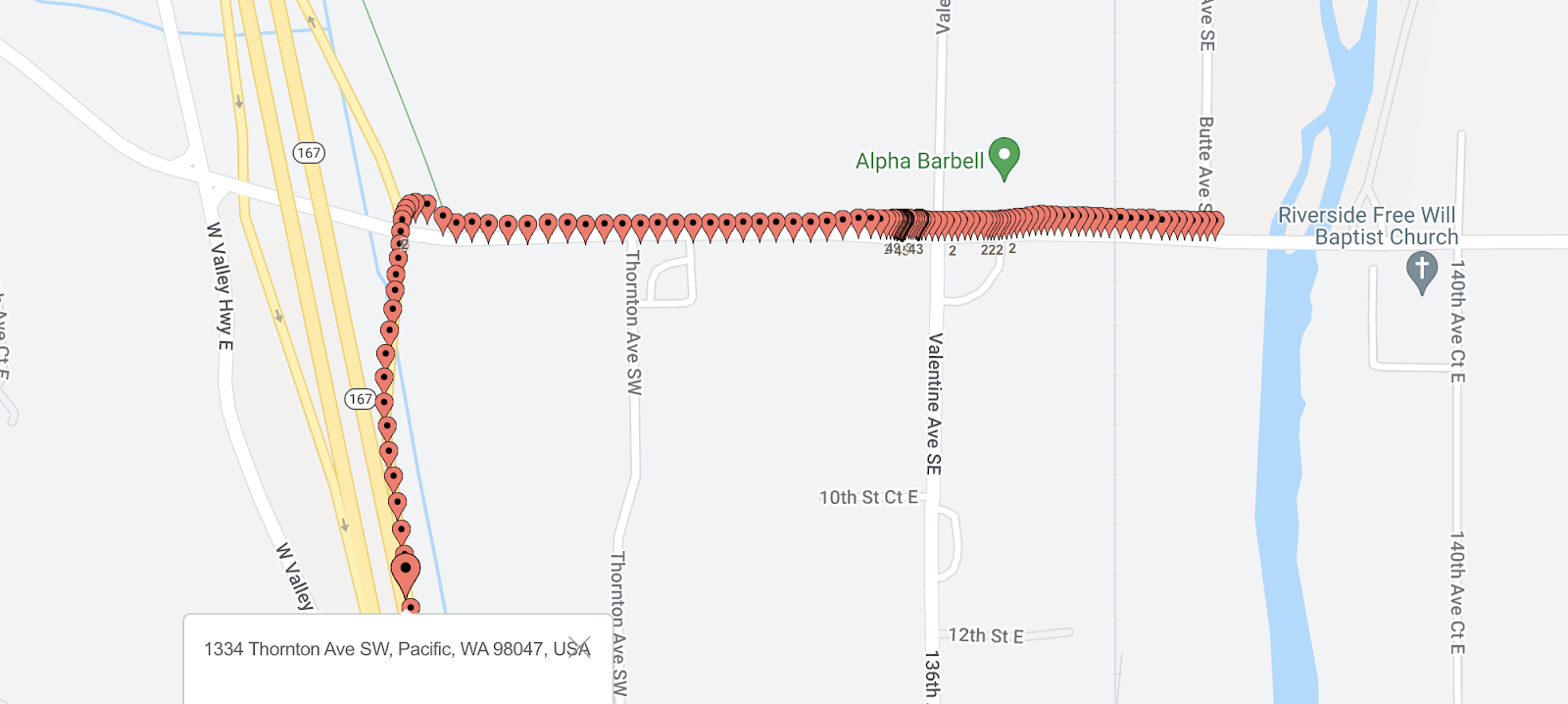
We initially changed the distance formula to ignore points that lay more than 100 miles off from an adjacent point. This fixed the problem of wild swings. However, it still resulted in the miles being artificially inflated. After a lot of trial and error, I changed the algorithm to ignore any point that fell more than a mile from the previous point. Since the phone would capture a point every few seconds, and our drivers aren’t flying at supersonic speeds, this was a pretty safe bet. This then presented us with a much more accurate picture.

But, there was this inherent assumption in this solution that ended up biting us on challenge 1. Are you curious what that was? Well, please read on.

So, say we have two adjacent points `p1` and `p2`, and they are 1.5 miles apart. We can ignore this 1.5-mile section, but on subsequent processing (since there are more points, `p3`, `p4` etc), do we ignore `p2` as an anomaly, or `p1`? Essentially, how do we know which point is “wrong”?

At first, I thought this was pretty obvious - since we were doing fine until we saw `p2`, that must be the culprit, so I ignored `p2` and kept going.

But do you see how that approach will not work for Challenge 1? Here, `p1` would be the last point we see in Redmond before Kate switches off the app. The very next point we see is `p2` in Seattle. Now if we ignore `p2` for processing the next set of points, and calculate the distance for all of these from `p1`, they are all going to be significantly higher than 1 mile, and they are all going to be excluded. The result would be pretty disappointing for Kate as we will show her as having zero deductible miles. (Yikes!)

This is not a theoretical scenario alone—this happened yesterday to a driver and we hit upon this on one of our manual testing binges. After pouring over the geo data, I could at least identify the reason we are producing low miles for this user.
‍

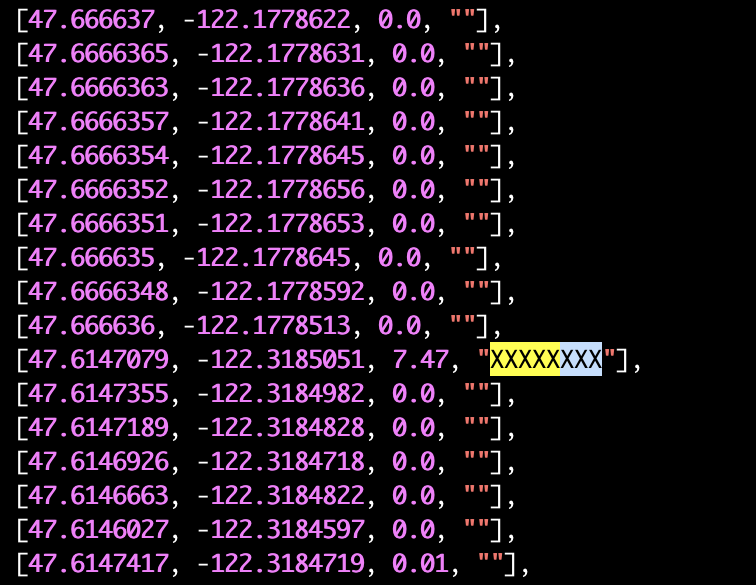
What you see above is a section of records we received for this user. It tabulates latitude, longitude, distance, and an XXXXXX marker for quick identification when the distance between adjacent points is over 1 mile. Notice the 7.47 miles that popped up due to the user traveling with the app turned off?

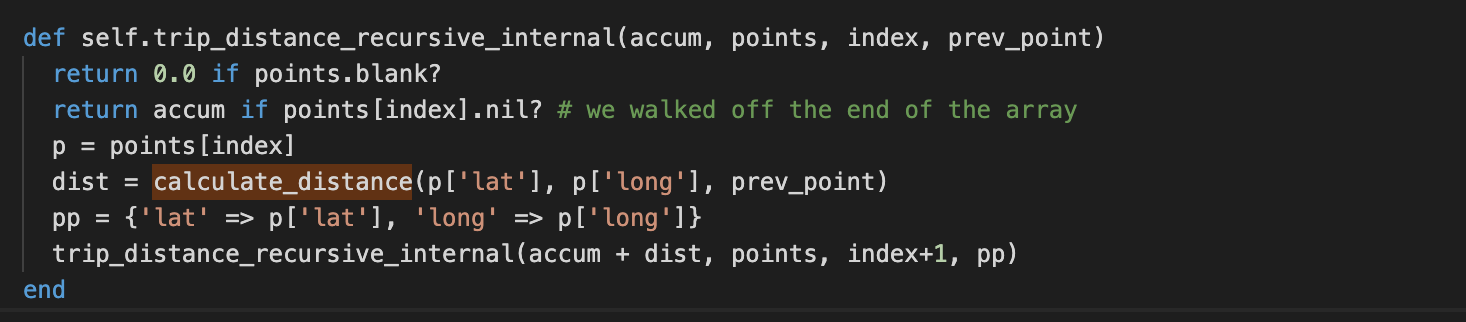
So, I thought that this calls for a slightly more complex algorithm that is recursive in nature. So, when we hit a geo point 1 mile out, we don’t know which point is actually “correct”, so we recursively compute both paths and then pick the path which has the highest miles. This seemed the correct approach as one path would increasingly not accumulate miles as each and every point would be more than 1 mile out.

Here is what that first attempt looked like (in Ruby):

Unfortunately, running this blew up the Ruby JVM stack. Ruby does not do a particularly good job in managing the stack, so I wasn’t too surprised. But of course, the first thing any programmer does (unless they are overconfident or a true genius, of which I try not to be the first and am definitely not the second), is to see if they have an infinite recursion bug in the code.

Note: `calculate_distance` computes the great-circle distance between points using the Haversine formula.

To make sure there was no bug lurking here, I implemented a fairly trivial recursion that computes the distance by recursing through all the points in the array. But, this still killed the Ruby stack so it was time to change tactics.

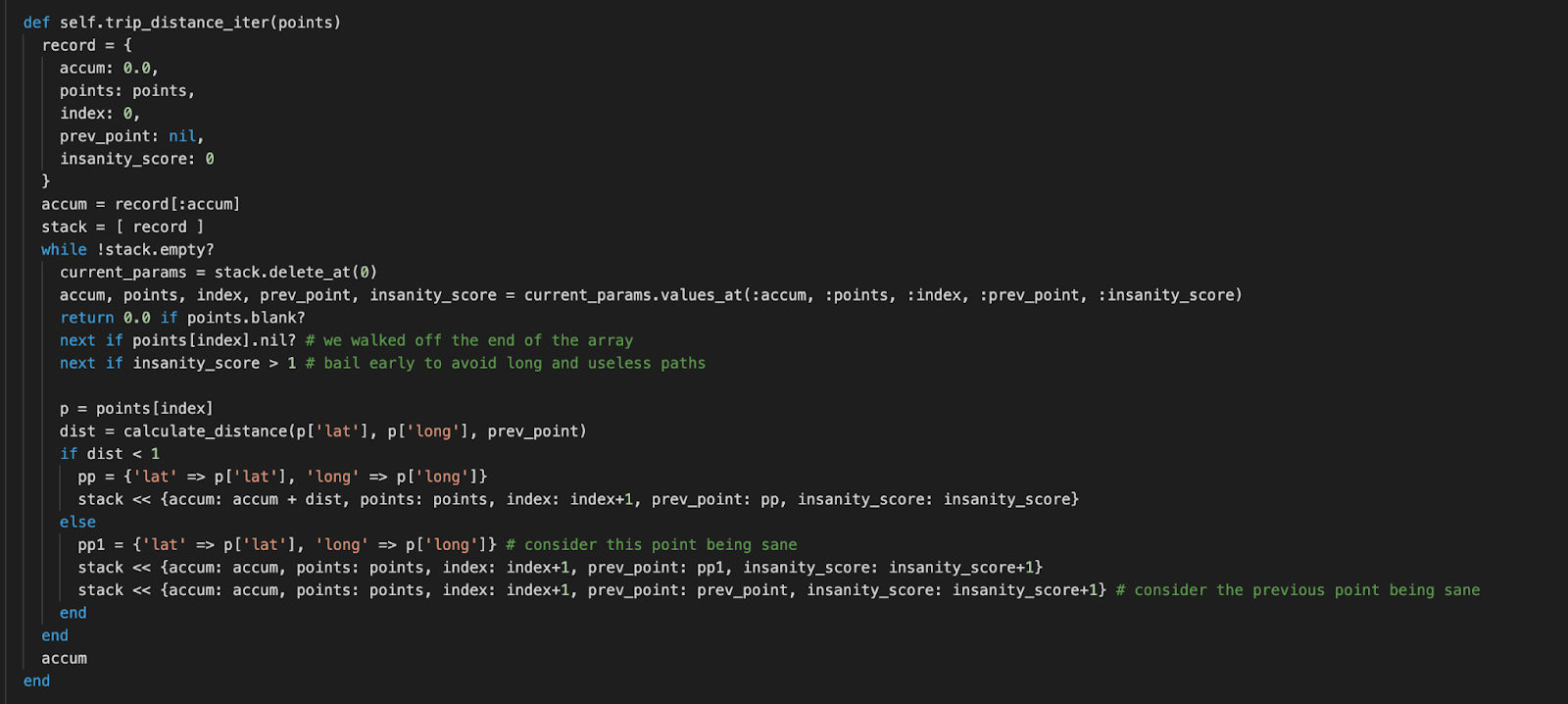
A recursive function can be changed to use a user-defined stack, which is what we did next. First, I did the simple implementation that added all points and made sure the result was what we expected. Since the iterative implementation cannot easily determine where users start working, I introduced an `insanity_score` that bails early if they are going down the wrong path. This has the advantage of limiting the execution time but is not as flexible as the recursive solution that in theory (under a JVM with a better-managed stack) can go down multiple paths all the way and pick the winners recursively.

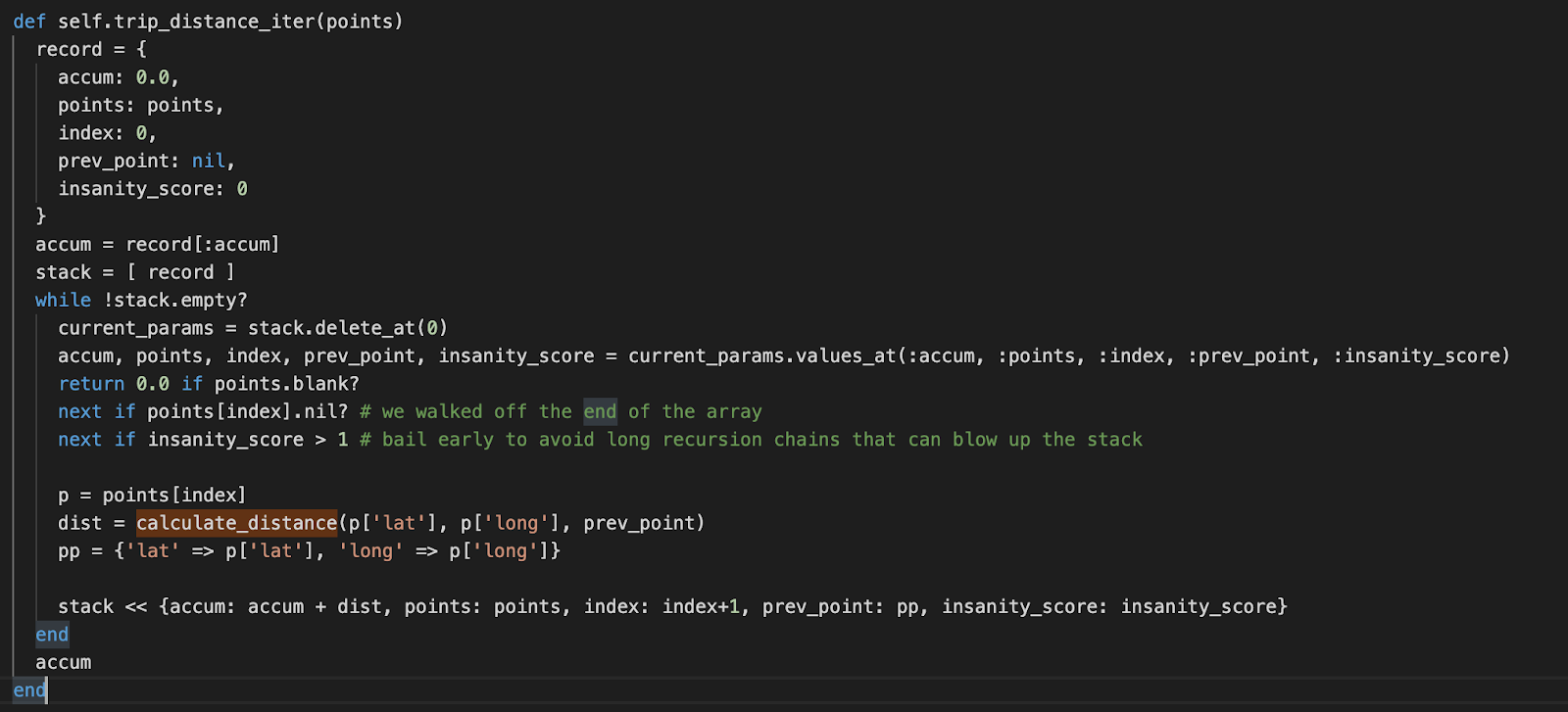
Here is the final algorithm that handles our use case:

To appreciate the drastic improvement in distance, here are the results from the earlier algorithm as compared to the new:
‍
Old Miles: 3.80
New Miles: 19.89
‍
Though these numbers may seem small, this equates to a 500% increase! This means users are no longer leaving money on the table when they go to deduct their miles when filing their taxes. Hopefully, this gives you some insight into the unique challenges in geo computing that the engineers at Solo work through in order to give our users an accurate picture of their expenses as we aim to maximize user take home pay.